Calcolare stanca

Se mai Nepero avesse dovuto sintetizzare in un motto pubblicitario il leit-motiv della sua ricerca, certo avrebbe scelto qualche cosa di simile all'espressione «calcolare stanca».

Ritratto di Nepero, autore ignoto,
National Portrait Gallery of Scotland

Egli fece di tutto per ovviare a questo inconveniente: costruì i logaritmi per risolvere i problemi di calcolo degli astronomi e, pensando ad esigenze più limitate, promosse la realizzazione di semplici strumenti che agevolassero il calcolo ripetitivo di moltiplicazioni e divisioni.

Così scrive Nepero stesso:
Eseguire dei calcoli è operazione difficile e lenta e spesso la noia che ne deriva e la causa principale della disaffezione che la maggioranza della gente prova nei confronti della matematica.
Ho cercato sempre - usando tutti i mezzi che avevo a disposizione e con le forze che il mio intelletto mi ha dato - di rendere più agevole e spedito questo processo.
È con questo scopo ben fisso nella mente che ho elaborato il metodo dei logaritmi, a cui ho dedicato molti anni di studio...
Nello stesso tempo, a beneficio di chi volesse far uso solo dei numeri naturali, ho predisposto altri tre brevi metodi di semplificazione dei calcoli. Il primo dei quali e stato battezzato Rabdologia e si basa sull'uso di alcune asticelle su cui sono scritti i numeri...

Rabdologia, p. 1

Ioanne Nepero, frontespizio Radbologia (Edimburgo,1617)

Il metodo "rabdologico" prevedeva l'uso di uno strumento costituito da una serie di dieci o più bastoncini che riportavano, utilmente suddivisa, la tavola pitagorica: i bastoncini erano generalmente realizzati in avorio.

Quest'ultima circostanza sta all'origine del loro nomignolo: infatti furono ribattezzati confidenzialmente "ossa" di Nepero ed a tutt'oggi questo è il nome con cui viene solitamente definito questo strumento di calcolo nei paesi di lingua anglosassone.

Bastoncini di Nepero c. 1760. Collezione privata

Le "ossa" si collocano a metà strada tra l'antico abaco e gli strumenti analogici più moderni che fanno la loro comparsa all'inizio del Seicento.

Nepero diede il nome di Rabdologia al libro che descrive lo strumento pensando le asticelle come una metafora del bastone del rabdomante (rabdos significa appunto bastone in greco): con i bastoncini, le "Ossa" di Nepero, non si trova l'acqua ma una soluzione rapida delle quattro operazioni!

La Rabdologia fu pubblicata nel 1617, in latino come già Nepero aveva fatto per le opere precedenti. Il successo del libro e delle "ossa" in esso descritte fu immediato: ne uscirono ben presto delle traduzioni in inglese, francese, tedesco ed italiano. Possedere il nuovo strumento di calcolo ben presto diventò un irrinunciabile cult per gli intellettuali della seconda metà del Seicento.

I bastoncini

La Rabdologia è l'arte di calcolare tramite bastoncini numerati: si tratta di righelli facilmente maneggiabili.

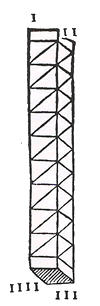Illustrazione schematica di un bastoncino

Ogni faccia longitudinale è divisa in dieci parti uguali, nove parti all'interno e una decima suddivisa in due metà poste ai due estremi.

La scelta della sezione quadrata rende disponibili su ogni righello quattro facce uguali su cui disporre, uno sotto l'altro i multipli dei numeri da 1 a 9, come nelle usuali tavole pitagoriche: rende anche possibile affiancare un righello all'altro.

Ognuno dei nove quadratini è, a sua volta diviso con la diagonale in due triangoli uguali: per ciascun numero la cifra delle decine si colloca nel triangolo di sinistra, quella delle unità in quello di destra.

L'abbinamento delle numerazioni da inserire nelle facce di uno stesso righello non è casuale, come pure l'ordine ascendente o discendente secondo cui disporre i multipli lungo una stessa faccia.

Le facce del primo bastoncino

Raddoppiare, triplicare

I righelli con la loro sequenza di multipli consentono agevolmente di raddoppiare, triplicare, in genere moltiplicare un numero per un fattore da 2 a 9.

Come fare è semplice, forse neanche tanto vantaggioso valutando che il tempo e la fatica che si impiegano con carta e matita non sono molto diversi da quelli che si impiegano servendosi delle "Ossa".

La differenza, a vantaggio dell'uso delle "Ossa", può forse dipendere da una consolidata abitudine a servirsi dello strumento e, quindi, dalla velocità che si acquisisce nel suo uso.

Vediamo come operare per raddoppiare il numero 1615, anno in cui lo strumento era certamente apprezzato:

A. si affiancano quattro righelli che iniziano per 1, 6, 1, 5;

B. nella prima riga relativa ad essi si legge, naturalmente 1615;

C. nella seconda riga si leggono 0/2 1/2 0/2 1/0 (la linea obliqua non rappresenta una frazione ma è l'eseplificazione grafica della posizione dei numeri sulle facce di ciascun bastoncino)

D. appaiando le cifre adiacenti si ha
0/[2 + 1]/[2 + 0]/[2 + 1]/[0]

E. sommando le cifre appaiate si ottiene 3230, esattamente il doppio di 1615.

Ove si volesse leggere il triplo basterebbe leggere la terza riga 0/3 1/8 0/3 1/5, appaiando analogamente le cifre 0/[3 + 1]/[8 + 0]/[3 + 1]/[5] = 4845

La quarta riga porterebbe 0/[4 2]/[4 0]/[4 2]/[0] = 6460

È evidente come la scrittura nei bastoncini dei numeri separando la cifra delle decine da quella delle unità agevoli le normali operazioni di riporto.